Although this page is often accessed as a stand-alone piece, it is part of a work on the history of the British and Irish cement industries, and where statements are made about the historical development of techniques, these usually refer only to developments in Britain.
Liquid production
As mentioned above, the aluminate and ferrite make no significant contribution to the strength of the product, and are present solely for the convenience of the manufacturer, providing the liquid in the burning zone of the kiln that allows the completion of alite formation at an economically viable temperature. The amount of liquid that can form is conventionally calculated using the Lea and Parker equation: at 1400°C, the amount of liquid produced is given by:
L1400 = 2.95 Al2O3 + 2.2 Fe2O3 + M
where M is equal to the %MgO if MgO<2%, otherwise M = 2.
The final reaction which occurs during clinker formation, and requires the peak temperature of the kiln, is the reaction of belite with excess calcium oxide to form alite:
Ca2SiO4 + CaO → Ca3SiO5
or more correctly:
[Belite] + CaO → [Alite]
The degree to which this conversion is completed in the finished clinker can be expressed as a quantity k where:
k = [Alite] / { [Belite] × [Free CaO] }
The bracketed quantities are mass %. k varies with peak temperature t(°C) according to the familiar equation:
ln(k) = s - h / (t + 273.15)
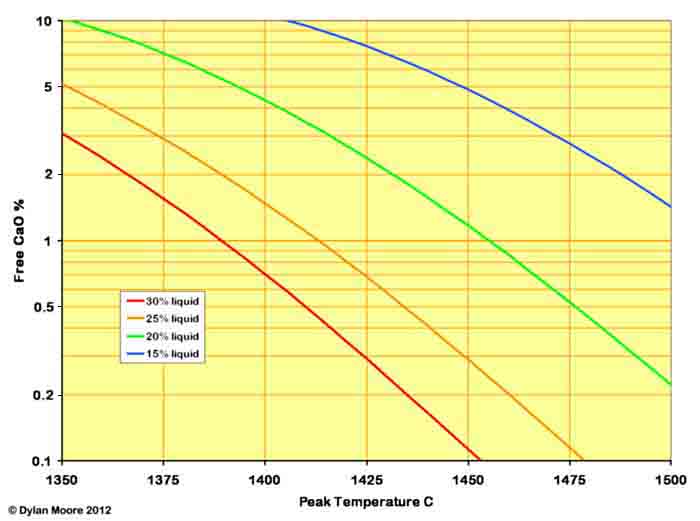
The value of h is usually around 120,000. s varies depending upon the fineness and homogeneity of the rawmix and the amount of liquid. For a typical well-prepared rawmix, the free lime varies as follows:
The effect of increasing the liquid production is to lower the temperature at which an acceptable level of free lime can be achieved. This provides two benefits for the manufacturer:
- a lower energy consumption can be achieved.
- an increase in the temperature difference between the flame (~1900°C) and the clinker increases the rate of heat exchange in the burning zone and therefore increases output.
The effect of increased liquid on the properties of the resulting cement are:
- more rapid strength development due to smaller and more defective crystals of silicate produced at lower temperature.
- a proportionally lower ultimate strength due to dilution by aluminate and ferrite.
- an increase in the deleterious effects of aluminate and ferrite discussed above.
- at higher levels of liquid, an increased tendency to block the kiln (or reduce its capacity) with excessive coating.
Alite content
The expression for k above shows that a higher processing temperature is needed if the alite content is raised. This, of course, is the essence of the discovery made by William Aspdin in the 1830s: making Portland cement, of which alite is the characteristic mineral, requires a higher temperature. By reducing the alite content, kiln output can be increased, but at the expense of a dramatic reduction in the reactivity of the cement.
Rawmix fineness
The fineness and homogeneity of the rawmix have a profound effect upon burnability. This is discussed under Raw Material Preparation. The most significant effect is the size of quartz particles in the rawmix: quartz particles above 45 μm in diameter considerably increase the temperature at which combination can be achieved. If liquid is reduced by replacing alumina and iron with silica, and the silica source in the rawmix includes coarse quartz, the resulting increase in burning temperature can be much greater than that discussed above.
Theoretical Enthalpy
Because both the starting materials and the end products are complex and often of indeterminate composition, tailor-made thermochemical data are not available. However, in practice, the system's thermochemical behaviour can be accurately assessed by assuming that the starting materials and end products have simplified chemical composition. For example, a rawmix can be thought of as comprising such minerals as quartz, kaolinite, calcite, magnesite etc., while the clinker can be thought of as containing tricalcium silicate and dicalcium silicate rather than the more complex alite and belite. Data on suitable start- and end-product minerals can be found in the Minerals Table. This approach to thermochemistry was first attempted by zur Strassen in the 1930s, although understanding of the system has evolved somewhat since then, and somewhat better thermodynamic functions are now available.
The energy that must be input in order to make clinker is conventionally calculated from standard enthalpies of formation of the input and output materials in their standard state: viz. at 25°C (298.15 K) and at a pressure of 1 standard atmosphere (101325 Pa). The actual energy input in the manufacturing process consists of this "theoretical heat of reaction" plus heat lost due to inefficient heat transfer (i.e. materials leaving the system above the standard temperature) and heat escaping from the system (i.e. shell losses).
The "theoretical heat" is calculated from the clinker chemical analysis. From this one calculates the amount of each of a set of notional "compounds" that make up the clinker: this set consists of the "Bogue" phases and a further set of compounds that account for the disposition of the minor elements in the clinker. One also calculates the amounts of a set of notional compounds that might have made up the rawmix. An equation can then be drawn up:
{rawmix compounds} + SO2 + O2 → {clinker compounds} + H2O + CO2
The coefficients in this equation can then be multiplied by the standard enthalpies of formation: the theoretical heat is the sum of the output enthalpies minus the sum of the input enthalpies.
Zur Strassen made similar calculations, using a simple set of standard minerals which allowed the derivation of a simple linear equation relating heat of reaction to the amount of each oxide in the clinker analysis. In practice, the equations are not quite linear, for a number of reasons. For instance, zur Strassen assumed that all magnesium starts out as magnesite (MgCO3) and ends up as periclase (MgO). However, the magnesium in clinker first goes into solid solution in the main clinker phases, and only after these are saturated does periclase form. The situation with alkali metals and sulfur is still more complex. Most obviously, the classical zur Strassen equation had no sulfur term, there being little sulfur in "old fashioned" clinkers, whereas sulfur is both prominent and variable in modern clinker. Zur Strassen also assumed that the main clay mineral was illite, which is far from being the case for British raw materials (and in fact for most raw materials world-wide that are derived from normal continental sediments). Nevertheless a simple equation is preferable, and can be derived by Montecarlo computation on a very large dataset of random clinker-like analyses.
The result of this calculation is sets of equations as follows:
where the main clay mineral is kaolinite (recommended):
H = -24.20 SiO2 + 1.0 Al2O3 - 1.4 Fe2O3 + 33.51 CaO + 38.4 MgO - 66.4 SO3 + 23 Na2O + 6.3 K2O - 34 TiO2 - 40 P2O5 - 3 Mn2O3
where the main clay mineral is pyrophyllite:
H = -24.19 SiO2 - 0.3 Al2O3 - 1.4 Fe2O3 + 33.49 CaO + 38.5 MgO - 66.4 SO3 + 25 Na2O + 7.8 K2O - 34 TiO2 - 40 P2O5 - 4 Mn2O3
The value of H is in kJ/kg. The oxide percentages are those in the loss-free clinker, normalised to 100.00%. If not all oxide values are available, then the calculation can be performed on the reduced set, again normalised, but bear in mind that in a typical clinker, the contributions of Ti, P and Mn lower the value by about 15 kJ/kg. It will be noticed that the sulfur term has by far the largest absolute magnitude, sulfur being the most electronegative element considered.
On the typical clinker (analysis given above) the first equation gives 1719 kJ/kg.
Reaction Stages
The rawmix enters a kiln system at a temperature close to ambient, and the temperature rises as it passes through the kiln system until it reaches a peak temperature in the sintering zone, after which the chemical state of the clinker is frozen by rapid cooling. During the process of temperature rise, chemical reactions take place in sequence. It is convenient to treat these reactions as if they occur within sharply-defined temperature ranges, although in practice the reaction stages often overlap considerably. A convenient set of reaction stages is as follows:
- 65-125°C Free water evaporates: latent heat must be supplied.
- 400-650°C Clays decompose endothermically, and alkalis react with the kiln atmosphere to form liquid sulfates.
- 500-650°C Dolomite decomposes endothermically.
- 650-900°C Calcium carbonate reacts endothermically with silica to form "incipient belite".
- 700-900°C Calcium carbonate reacts endothermically with alumina and iron oxide to form incipient aluminate and ferrite.
- 900-1050°C When all available silica, alumina and iron oxide have reacted, the remaining calcium carbonate decomposes endothermically to calcium oxide.
- 1300-1425°C Aluminate, ferrite and part of the belite melt endothermically, and belite reacts with calcium oxide to form alite.
- 1425-1300°C Having passed peak temperature, the melt re-freezes exothermically to aluminate, ferrite and belite.
These stages are treated in detail below.
1. 65-125°C: Evaporation of free water. Water, of course, boils at 100°C, but can be evaporated at lower temperatures by a current of gas, provided that the partial pressure of water in the gas is below water's vapour pressure. In a wet kiln, with an exhaust gas containing 40-50% water vapour by volume, this condition is met when the temperature is 76-82°C, but because the exhaust gas is typically at above 170°C, evaporation still occurs at the surface at lower temperatures, and in practice the evaporation rate becomes substantial when the slurry temperature is in the mid-60s. In real kilns, the temperature does not flatten off when it reaches 100°C, but keeps on rising steadily. This is because of the labyrinthine path that water molecules have to follow in escaping from the cohesive mass of slurry. A pressure above atmospheric is required to drive it along this path, and the water becomes superheated. The evaporation rate only tails off when the feed temperature rises above 120°C. The enthalpy change at 25°C is +43.989 kJ/mol: at 100°C it is +40.865 kJ/mol. The typical clinker mentioned above has 1.5429 kg of notional dry rawmix per kg clinker made, and if this takes the form of a slurry with 38% free moisture, then 0.9456 kg (52.49 mol) of water must be evaporated, with a heat input of 2145 kJ/kg clinker. Note that this is considerably more than the "theoretical heat of reaction" given above: this is the principal reason for the inherent inefficiency of the Wet Process.
2. 400-650°C: Clay decomposition. There are many clay minerals in cement rawmixes, but their behaviour can be adequately modelled by focusing on the most common one - kaolinite, Si2Al2O5(OH)2. Although the thermal behaviour of kaolinite is complex, from the cement manufacturing point of view, the effective formula is:
Si2Al2O5(OH)2 → 2 SiO2 + Al2O3 + 2 H2O (vapour)
The enthalpy change for this at 25°C is +139.3 kJ/mol: at 525°C it is +113.7 kJ/mol.
"Clay" minerals also accommodate most of the alkalis in a rawmix. Again, the situation is complex, but an adequate account can be based on the assumption that they exist as alkali feldspars. In isolation, feldspars do not decompose at such a low temperature, but in the conditions of the cement kiln, alkalis become detached and will usually react immediately with the acid gases of the kiln atmosphere. An equation describing this might be:
KAlSi3O8 (orthoclase) + 0.5 SO2 + 0.25 O2 → 3 SiO2 + 0.5 Al2O3 + 0.5 K2SO4
The enthalpy change for this at 25°C is -219.7 kJ/mol: at 525°C it is -208.8 kJ/mol. The corresponding data for the sodium analogue (albite) are -167.5 and -151.0.
1 kg of the typical clinker described above requires a notional 0.1258 kg (0.4873 mol) of kaolinite in its rawmix, so an energy input of 55.4 kJ is required. Similarly, a notional 0.01608 kg (0.0307 mol) of albite and 0.02286 kg (0.0411 mol) of orthoclase are required, and their reactions evolve 4.6 and 8.6 kJ respectively, so the nett energy input of the stage is 42.2 kJ/kg clinker.
3. 500-650°C: Dolomite decomposition. Dolomite - CaMg(CO3)2 - is the mineral containing the part of the rawmix magnesia existing as carbonates. Most clays also contain magnesia as various silicates, and low magnesia rawmixes, such as are typical in southeast England, contain little magnesia in carbonate form. Dolomite is a distinct compound, thermodynamically more stable than the corresponding mixture of carbonates. However, its thermal decomposition proceeds in a manner indistinguishable from that of a mixture: decomposition begins at essentially the same temperature as magnesite (MgCO3) and leaves calcium carbonate:
CaMg(CO3)2 → CaCO3 + MgO + CO2
The enthalpy change for this at 25°C is +128.4 kJ/mol: at 575°C it is +122.3 kJ/mol.
For convenience, non-carbonate magnesium compounds can be thought of as reacting in this temperature range as well. For example, phlogopite might react as follows:
KMg3AlSi3O10(OH)2 + 0.5 SO2 + 0.25 O2 → 0.5 K2SO4 + 3 MgO + 0.5 Al2O3 + 3 SiO2 + H2O (vapour)
The enthalpy change for this at 25°C is -111.2 kJ/mol: at 575°C it is -106.1 kJ/mol.
1 kg of the example clinker includes 0.0365 kg (0.1981 mol) of dolomite and 0.0180 kg (0.0431 mol) of phlogopite (or its equivalent) in its rawmix, so nett energy input is 24.2 - 4.5 = 19.7 kJ.
4. 650-900°C: Low temperature calcite decomposition. Calcite is the usual form of calcium carbonate in cement rawmixes - aragonite is occasionally encountered, but not in Europe. Its decomposition is central to much of the discussion in this website - it evolves carbon dioxide in quantities exceeding half the mass of the finished clinker, and requires a large energy input. The large scale of the reaction's endotherm means that this stage of the process takes up a major part of the cement kiln, and the efficiency with which the reaction is achieved is a major factor in defining the output and heat consumption of the kiln.
Pure calcite decomposes (i.e. the pressure of carbon dioxide in equilibrium with it reaches atmospheric) at 1169 K (approximately 896°C).
A wide range of temperature values are found in the literature. Despite the importance of the reaction, the state of knowledge is still poor, perhaps because it is difficult to determine equilibria in a reaction that is not smoothly reversible, and also because of the extraordinary difficulty in getting calcite samples of adequate purity. The above is derived from the best available internally consistent thermodynamic functions.
A current of hot air, with a CO2 partial pressure of 40 Pa, can remove carbon dioxide at 536°C, but kiln gases contain perhaps 35% CO2, and would decompose pure calcite only above 829°C. In reality, in a kiln burning a normal cement rawmix, decomposition begins at around 650°C. This, put simply, is because the clay components (or their decomposition products) act as an acid. The reaction is:
2 CaCO3 + SiO2 → Ca2SiO4 + 2 CO2
The product of the reaction is "incipient belite" - so called because the early reaction products are "amorphous", and not identifiable as crystalline species by microscopy or x-ray diffraction. However, the endotherm is essentially that of the above reaction.
It should be understood that dicalcium silicate is very stable, and can easily be made at temperatures much lower than 500°C from a mixture of fine silica and a low-temperature lime source such as calcium oxalate. Interestingly, the same effect was independently discovered by the researchers developing the Anhydrite Process. They found that the decomposition temperature of anhydrite could be lowered by 100°C by adding finely-ground sand, and by 300°C by adding finely-ground shale.
Key to this reaction is the availability of reactive clay decomposition products, and of small amounts of alkali sulfate/chloride melt, which draw the reactants together by surface tension and act as an ion transfer medium. An important point to note is that at this stage, no free calcium oxide forms, provided that the rawmix is reasonably fine. This behaviour is normal in kilns: the mix loses CO2, but free lime is low until the next reaction stage. This stage ends when all the available silica is used up.
The assumption that all the silica is used up by the time the temperature reaches 900°C is more or less correct if the silica is fine. If some of the silica is grossly oversized, a considerably higher temperature may be needed to complete the reaction, but in any case reaction is complete below 1300°C.
The enthalpy change for this reaction at 25°C is +230.16 kJ/mol: at 775°C it is +210.99 kJ/mol.
A certain amount of magnesia ends up in the silicate phases, and the MgO produced in the last stage can be thought of as reacting here with silica to produce forsterite (which will actually go into solid solution in the belite):
2 MgO + SiO2 → Mg2SiO4
The enthalpy change for this reaction at 25°C is -63.6 kJ/mol: at 775°C it is -65.4 kJ/mol.
Phosphorus usually exists in the rawmix as apatite. This will also react with a little free silica, producing whitlockite (which will also actually go into solid solution in the belite):
Ca5(PO4)3OH + 0.25 SiO2 → 1.5 Ca3(PO4)2 + 0.25 Ca2SiO4 + 0.5 H2O (vapour)
The enthalpy change for this reaction at 25°C is +100.7 kJ/mol: at 775°C it is +104.1 kJ/mol.
After the previous stages, we consider that all the silica in the rawmix, originally in quartz, kaolinite, albite, orthoclase and phlogopite, is now in the form of SiO2, ready to react. There is 0.2153 kg (3.5833 mol) of silica in 1 kg of the example clinker. The magnesia that ends up in the clinker silicates is equivalent to 0.0168 kg (0.1194 mol) of forsterite. The apatite content of the rawmix is 0.0026 kg (0.0052 mol). These two use up 0.1246 mol SiO2, leaving 3.4587 mol for the main reaction. The nett heat input for this is 729.8 - 7.8 + 0.5 = 722.5 kJ.
5. 700-900°C: Alumina and iron oxide react. Here calcium carbonate continues to react in a concerted manner with the other oxides, without any intervening calcium oxide formation. Although tricalcium aluminate is stable in this temperature range, mayenite (Ca12Al14O33) seems to be the mineral formed, although again it is poorly crystallized. Alternative assumptions make little difference to the thermal calculations. The behaviour of manganese is indistinguishable from that of iron.
12 CaCO3 + 7 Al2O3 → Ca12Al14O33 + 12 CO2
The enthalpy change for this reaction at 25°C is +2060 kJ/mol: at 800°C it is +1892 kJ/mol.
4 CaCO3 + Al2O3 + Fe2O3 → Ca4Al2Fe2O10 + 4 CO2
The enthalpy change for this reaction at 25°C is +661.9 kJ/mol: at 800°C it is +611.8 kJ/mol.
4 CaCO3 + Al2O3 + Mn2O3 → Ca4Al2Mn2O10 + 4 CO2
The estimated enthalpy change for this reaction at 25°C is +663.2 kJ/mol: at 800°C it is +631.6 kJ/mol.
1 kg of the example clinker contains by this stage sufficient reactants to produce 0.0859 kg (0.0619 mol) of mayenite, 0.0697 kg (0.1434 mol) of the ferrite and 0.0018 kg (0.0038 mol) of the manganite. Thus the nett heat input is 117.1 + 87.7 + 2.4 = +207.2 kJ.
6. 900-1050°C: The remaining calcite decomposes thermally. By this stage, only 0.3625 kg (3.6222 mol) of calcium carbonate remain, and decomposition proceeds, forming, for the first time, free lime:
CaCO3 → CaO + CO2
The enthalpy change for this reaction at 25°C is +178.31 kJ/mol: at 975°C it is +166.17 kJ/mol. 1 kg of the example clinker requires a heat input of 601.9 kJ.
7: 1300-1425°C Sintering. After the previous stage, nothing significant happens until a temperature of about 1300°C is reached. This is the eutectic melting point of the aluminate, ferrite and silicate mixture that forms the clinker "flux". The actual melting point varies: in the absence of "minor" oxides, particularly MgO and alkalis, the melting point is 1338°C, but in most mixes the MgO concentration is sufficient to lower the melting point to 1300°C. The rate at which melting takes place also varies. If the mix has the "eutectic composition" with an Al2O3/Fe2O3 ratio of 1.4-1.5 (depending on MgO content), most of the liquid forms at the melting point, but if the ratio deviates on either side of this value, melting is progressive as temperature rises.
Alite becomes stable above 1250°C, but only begins to form when liquid is formed. As with the low temperature melts in Stage 4 above, in addition to functioning as a solvent for exchange of ions between the solid phases, the liquid also physically draws the reactant particles together by surface tension, and a feed that was before powdery or granular now quickly consolidates into spherical nodules of clinker.
Only one chemical reaction need be described: belite reacts with free lime to form alite:
Ca2SiO4 + CaO → Ca3SiO5
This, of course, is the defining reaction of Portland cement manufacture. The enthalpy change for this reaction at 25°C is +13.4 kJ/mol: at 1360°C (a typical "half-way" temperature) it is +24.2 kJ/mol. 1 kg of the example clinker contains 0.6538 kg (2.8935 mol) of notional Ca3SiO5, and so requires a heat input of 69.3 kJ.
The minor phases mostly end up in the melt, and emerge from that, after cooling, metamorphosed, so for instance the original aluminate enters as Ca12Al14O33 but emerges as Ca3Al2O6. Several such disproportionations take place with complex interactions, but the nett effect is almost thermally neutral: the nett effect of these for 1 kg of the example clinker is a heat input of 32.0 kJ, but this is drowned in the major endotherm required for the latent heat of fusion. The latent heats of individual components of the melt seem never to have been determined, but the overall latent heat of melt-formation in real-world clinkers can be deduced from empirical "sensible heat" curves, and is around 440 kJ per kg of liquid or around 110 kJ per kg of clinker if liquid formation is a typical 25%. The nett effect of these heat flows is a heat input of 69.3 + 32.0 + 110 = 211.3 kJ/kg during the rise from 1300°C to the peak temperature, and an outflow of 110 kJ/kg (the latent heat) as the temperature falls back to 1300°C.
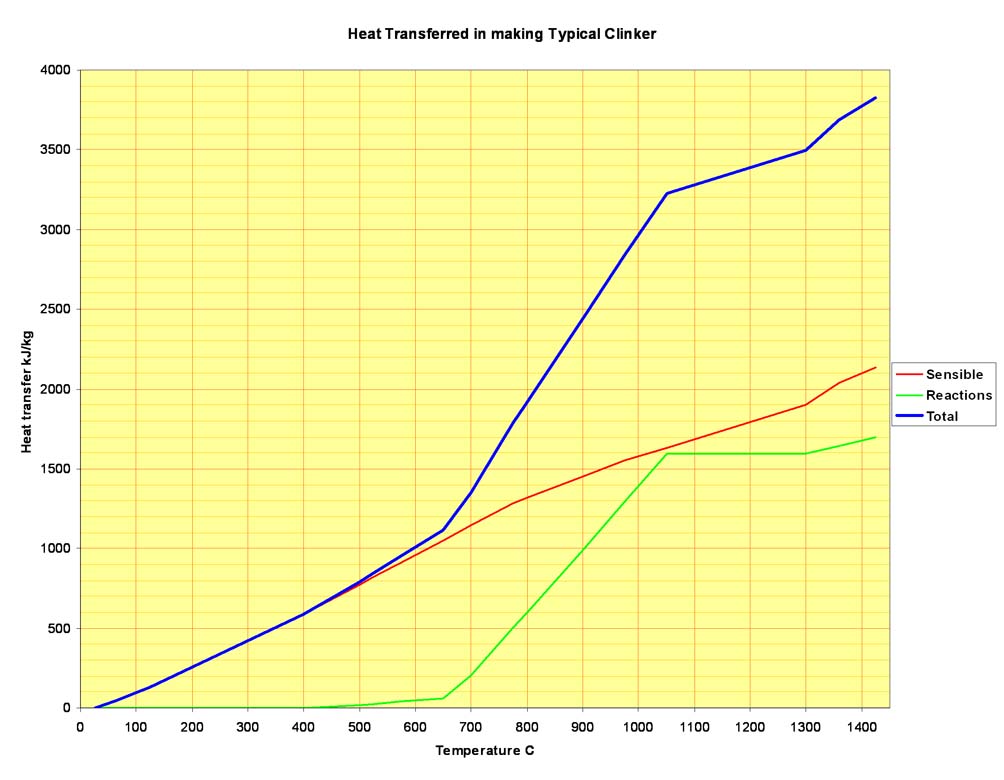
Putting all these stages together, it is possible to map out the heat flow into the feed material throughout the kiln. In addition to the reaction endotherms, the sensible heat required to raise the feed temperature must be taken into account. The latter, easily calculated from the enthalpy functions of the reactants at each stage, is greater than the heat of reaction. In the example clinker, the total sensible heat transferred to the feed in rising from 25 to 1425°C is 2134 kJ/kg, while the sum of the reaction endotherms at the reaction temperatures is 1695 kJ/kg. Of course, in an efficient kiln system, most of the sensible heat is subsequently recuperated and re-cycled. Plotting total heat transfer against temperature, we have this:
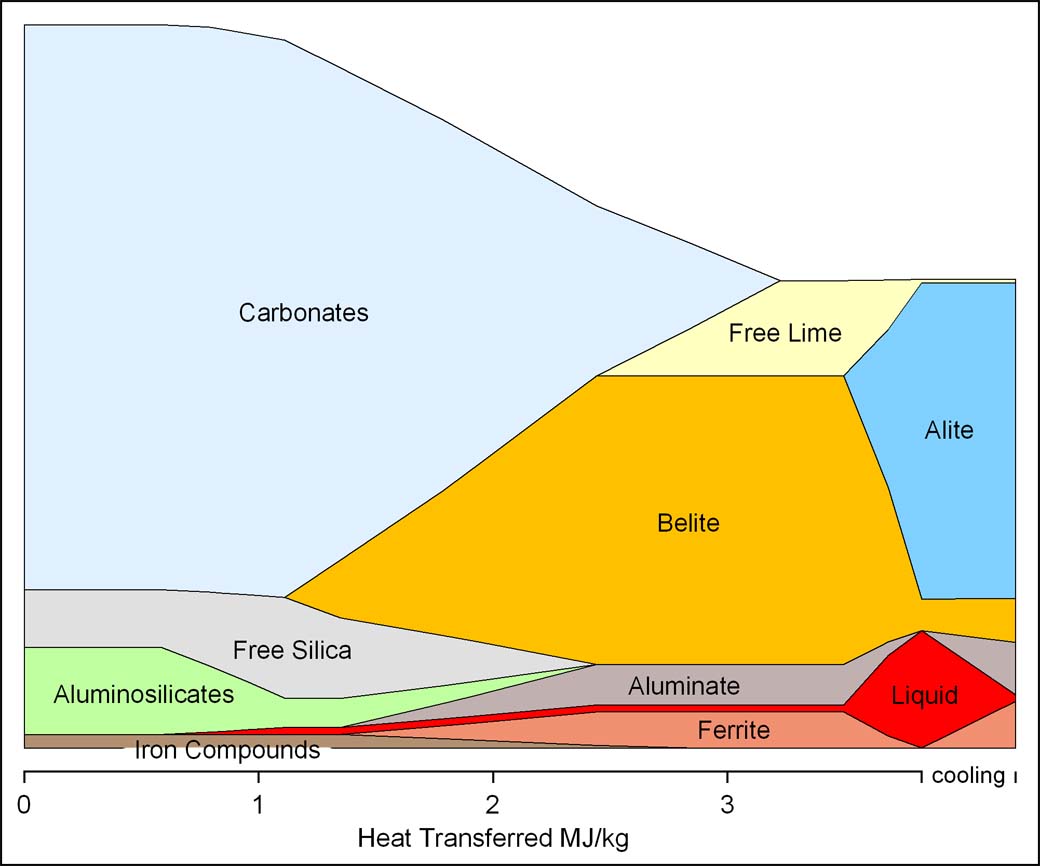
Using the total heat transfer calculated above as a "reaction coordinate", the changes in mass of the feed minerals can be plotted to summarise the reactions: